2. 시작하기
많은 알고리즘에서는 루프를 사용하여 문제를 해결하곤 한다.
우리는 코드가 문제없이 작성 되었다면, 그 루프가 정상적으로 작동하여 문제를 해결할 것을 알고 있다.
그러나 이를 논리적으로 증명하기는 어려웠다.
이때 사용할 수 있는 것이 루프 불변성(Loop Invariant)이다.
루프 불변성은 루프를 사용한 알고리즘이 타당(correct)한지 증명하기 위해 사용된다.
루프 불변성임을 확인하기 위해서는 세 가지 특성이 만족되어야 한다.
초기조건 : 루프가 첫 번째 반복을 시작하기 전에 루프 불변성이 참이어야 한다.
유지조건 : 루프의 반복이 시작되기 전에 루프 불변성이 참이었다면, 다음 반복이 시작되기 전까지도 계속 참이어야 한다.
종료조건 : 루프가 종료될 때 그 불변식이 알고리즘의 타당성을 보이는데 도움이 될 유용한 특성을 가져야 한다.
2.1 삽입정렬
반복문을 사용하는 삽입정렬 코드를 보며 루프 불변성에 대해 알아보자.
초기조건 : 루프의 첫 반복이 시작하기 전, A[1 .. j - 1]은 바뀌지 않은 A[1]인 한 개의 원소로 구성되므로, 루프 불변성이 성립한다.
유지조건 : 루프가 반복하면서 A[j] 원소를 A[1 .. j - k] 부분 배열의 알맞은 자리에 끼워 넣어 정렬시킨다. A[1 .. j] 배열은 정렬되기 전과 그 이후에도 동일한 원소를 갖기 때문에 루프 불변성이 성립한다.
종료조건 : 루프는 j가 A.length (= n) 보다 커지면 종료된다. A[1 .. n - 1] 배열은 A 전체 배열이며, A[1 .. n - 1] 배열은 루프가 시작되기 전과 동일한 원소지만 정렬된 순서로 저장되었다. 그러므로 삽입정렬 알고리즘은 타당하다.
import java.util.Arrays;
public class InsertionSort {
public static void insertionSortAsc(int[] testCase) {
for (int j = 1; j < testCase.length; j++) {
int key = testCase[j];
int i = j - 1;
while (i >= 0 && testCase[i] > key) {
testCase[i + 1] = testCase[i];
i--;
}
testCase[i + 1] = key;
}
}
public static void insertionSortDesc(int[] testCase) {
for (int j = 1; j < testCase.length; j++) {
int key = testCase[j];
int i = j - 1;
while (i >= 0 && testCase[i] < key) {
testCase[i + 1] = testCase[i];
i--;
}
testCase[i + 1] = key;
}
}
public static void main(String[] args) {
int[] testCase = {5, 2, 4, 6, 1, 3};
insertionSortAsc(testCase);
System.out.println(Arrays.toString(testCase));
}
}
2.2 알고리즘의 분석
알고리즘의 수행시간을 분석할 때에는 일반적으로 worst case를 기준으로 둔다.
그 이유는 해당 시간이 모든 입력에 대한 상한임을 보증할 수 있고, 의외로 최악의 경우가 종종 발생하기 때문이다.
2.3 알고리즘의 설계
알고리즘을 설계하는 방법에는 여러가지가 있다.
앞에서 알아본 삽입 정렬은 점진적인 방법으로 해를 구한다.
임의의 원소 A[j]를 정렬된 A[1 .. j-1]의 적절한 위치에 삽입하여, 정렬된 A[1 .. j] 배열을 만들기 때문이다.
이 외에 자주 사용되는 방법은 분할 정복이다.
말 그대로 문제를 유사하지만 크기가 작은 부분 문제로 분할하고, 이를 재귀를 통해 모두 푼 후에 해를 결합하여 원래 문제의 해를 구하는 방법이다.
조금 더 짜임새 있게 정리하자면, 세 단계로 구성할 수 있다.
분할 : 현재의 문제를 같은 문제를 다루는 다수의 부분 문제로 분할한다.
정복 : 부분 문제를 재귀적으로 풀어서 정복한다. 부분 문제의 크기가 충분히 작으면 직집적인 방법으로 푼다.
결합 : 부분 문제의 해를 결합하여 원래 문제의 해가 되도록 만든다.
분할정복의 대표적인 예시는 병합정렬이다.
아래의 코드를 통해 분할 / 정복 / 결합의 사례를 살펴보자.

public class MergeSort {
public static void merge(int[] A, int p, int q, int r) {
int n1 = q - p + 1, n2 = r - q;
int[] L = new int[n1 + 1], R = new int[n2 + 1];
for (int i = 0; i < n1; i++) L[i] = A[p + i];
for (int i = 0; i < n2; i++) R[i] = A[q + i + 1];
L[n1] = Integer.MAX_VALUE;
R[n2] = Integer.MAX_VALUE;
int i = 0, j = 0;
for (int k = p; k <= r; k++) {
if (L[i] <= R[j]) {
A[k] = L[i++];
} else {
A[k] = R[j++];
}
}
}
public static void mergeSort(int[] A, int p, int r) {
if (p < r) {
// 분할 : O(1) ; 부분 배열의 중간위치 계산은 상수시간이 걸린다.
int q = (p + r) / 2;
// 정복 : 2T(n/2) ; 입력이 n인 문제에 대한 수행시간이 T(n)이고, 각 부분 문제의 크기는 n/2이기 때문이다.
mergeSort(A, p, q);
mergeSort(A, q + 1, r);
// 결합 : O(n) ; n개의 원소만큼을 돌면서 결합하기 때문이다.
merge(A, p, q, r);
}
}
public static void main(String[] args) {
int[] t = {5, 2, 4, 7, 1, 3, 2, 6};
mergeSort(t, 0, t.length - 1);
}
}
책에서는 편의를 위해 시작 인덱스를 1로 설정하여 가르치고 있다.
그러나 나는 불필요한 메모리 낭비를 위해 인덱스를 0으로 두어 구현하였다.
병합정렬 알고리즘의 수행시간을 살펴보자.
분할은 O(1), 정복은 2T(n/2), 결합에는 O(n)이기 때문에 T(n)에 대한 점화식을 다음과 같이 표현할 수 있다.
$$ T(n)= \begin{cases} \mathsf{\Theta}(1), & if\ \ n = 1 \\ 2T(n/2) + \mathsf{\Theta}(n), & if\ \ n > 1 \\ \end{cases} $$
위 점화식은 마스터 정리를 통해 T(n)을 $\mathsf{\Theta}(n \ lg \ n)$으로 표현할 수 있다.
그러나 아직 마스터 정리를 배우지 않았더라도, 직관적인 방법으로 T(n)이 $\mathsf{\Theta}(n \ lg \ n)$임을 도출할 수 있다.
먼저, c라는 상수를 “크기가 1인 문제를 푸는 데 걸리는 시간”, “배열의 원소 개수 당 분할과 결합 단계에서 걸리는 시간” 을 동시에 나타낼 수 있다고 정의하자.
(물론 정확히 같다고 표현할 수는 없다. 그러나 둘 중 더 오래 걸리는 시간을 해당 점화식의 상한으로, 더 짧게 걸리는 시간을 해당 점화식의 하한으로 구하면, 두 한계 모두 $n\ lg\ n$의 차수로 나타난다.)
$$ T(n)= \begin{cases} c, & if\ \ n = 1 \\ 2T(n/2) + cn, & if\ \ n > 1 \\ \end{cases} $$
그렇다면, T(n)은 다시 다음과 같이 나타낼 수 있다.

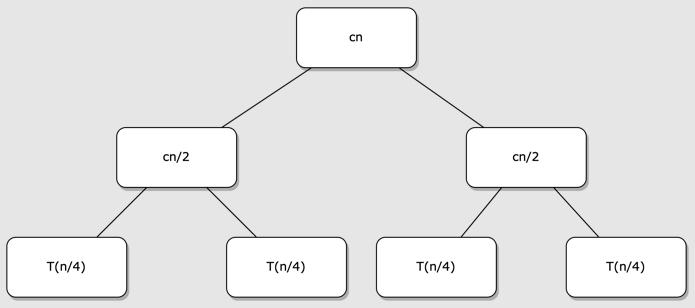
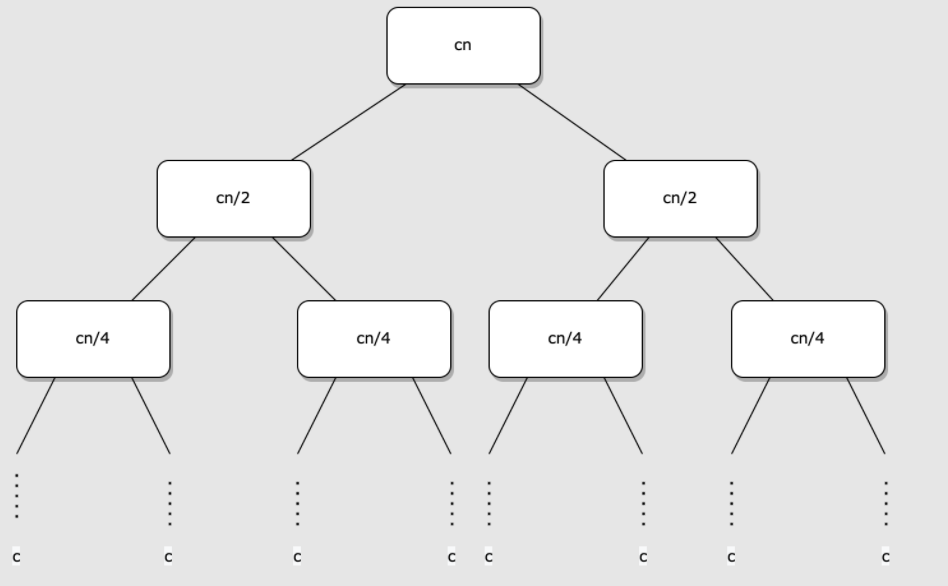
결과적으로 트리형태인 그림 c를 보자.
마지막 최하위 레벨에서는 노드가 n개 존재하고, 각각의 레벨에서 모든 노드의 합을 구하면 cn이 된다.
이러한 트리의 총 레벨 수는 $lg \ n + 1$ 이기 때문에, 레벨 당 비용 * 총 레벨 수를 곱해 총 비용 $cn (lg \ n + 1)$을 구할 수 있다.
여기서 낮은 차수항과 상수 c를 무시하면, $\mathsf{\Theta}(n\ lg\ n)$ 라는 결과가 나온다.
// 연습문제 2.3-1
// int[] A = {3, 41, 52, 26, 38, 57, 9, 49}
// mergeSort(A, 0, A.length - 1)
// 정답 :
Divide
{3, 41, 52, 26}
{3, 41}
{3} {41}
Conquer
{3} {41}
{3, 41}
A = {3, 41, 52, 26, 38, 57, 9, 49}
Divide
{52, 26}
{52} {26}
Conquer
{52} {26}
{26, 52}
A = {3, 41, 26, 52, 38, 57, 9, 49}
Conquer
{3, 41} {26, 52}
{3, 26, 41, 52}
A = {3, 26, 41, 52, 38, 57, 9, 49}
Divide
{38, 57, 9, 49}
{38, 57}
{38} {57}
Conquer
{38} {57}
{38, 57}
A = {3, 26, 41, 52, 38, 57, 9, 49}
Divide
{9, 49}
{9} {49}
Conquer
{9} {49}
{9, 49}
A = {3, 26, 41, 52, 38, 57, 9, 49}
Conquer
{38, 57} {9, 49}
{9, 38, 49, 57}
A = {3, 26, 41, 52, 9, 38, 49, 57}
Conquer
{3, 26, 41, 52} {9, 38, 49, 57}
{3, 9, 26, 38, 41, 49, 52, 57}
A = {3, 9, 26, 38, 41, 49, 52, 57}
// 연습문제 2.3-2
// 경계값을 사용하지 않도록 병합정렬을 재작성하라
// 정답 :
public class MergeSort {
public static void merge(int[] A, int p, int q, int r) {
int n1 = q - p + 1, n2 = r - q;
int[] L = new int[n1], R = new int[n2];
for (int i = 0; i < n1; i++) L[i] = A[p + i];
for (int i = 0; i < n2; i++) R[i] = A[q + i + 1];
int i = 0, j = 0;
for (int k = p; k <= r; k++) {
if (i >= n1) {
A[k] = R[j++];
}
else if (j >= n2) {
A[k] = L[i++];
}
else if (L[i] <= R[j]) {
A[k] = L[i++];
} else {
A[k] = R[j];
}
}
}
public static void mergeSort(int[] A, int p, int r) {
if (p < r) {
int q = (p + r) / 2;
mergeSort(A, p, q);
mergeSort(A, q + 1, r);
merge(A, p, q, r);
}
}
public static void main(String[] args) {
int[] t = {3, 26, 41, 52, 9, 38, 49, 57};
mergeSort(t, 0, t.length - 1);
}
}'CS > 알고리즘' 카테고리의 다른 글
| [Introduction to Algorithms] 4. 분할정복 (0) | 2022.02.14 |
|---|---|
| [Introduction to Algorithms] 3. 함수의 증가 (0) | 2022.02.12 |
| [Introduction to Algorithms] 1. 알고리즘의 역할 (0) | 2022.02.02 |
| 유클리드 알고리즘 (Euclid’s algorithm) (0) | 2021.11.03 |



