
3. 함수의 증가
앞서 배운 삽입정렬과 병합정렬의 수행시간을 생각해보자.
삽입정렬의 worst case는 $\mathsf{\Theta}(n^2)$이고, 병합정렬의 worst case는 $\mathsf{\Theta}(n \ lg \ n)$이었다.
그렇다면 병합정렬이 언제나 삽입정렬보다 우수한 알고리즘일까? 그것은 아니다.
이 표기는 상수와 저차항을 무시하여 표현된 것이기 때문이다.
만약 입력 n의 크기가 충분히 작다면, 상수와 저차항의 영향으로 오히려 삽입정렬이 더 우수한 결과를 내놓을 수도 있다.
반대로 입력의 크기가 충분히 커진다면, 상수와 저차항은 n에 묻혀버린다.
이렇듯 n의 크기에 따라 수행시간 표기가 역전되기도 한다.
그러나 역전이 가능한 경우의 수는 너무나도 적다. 또한, n이 작았을 때 얻을 수 있는 그 적은 비용이, 추후 n이 커졌을 때 얻은 비용보다 더 큰 비용을 초래하게 된다.

그래서 우리는 입력 n이 극한으로 커진 경우를 기준으로 점근적(asympotic) 효율성에 관해 다뤄볼 것이다.
3.1 점근적 표기(Asympotic notations)
가장 많이 사용되는 Big-oh 표기법부터 순서대로 알아볼 것이다.
[O-notation]
$$ O(g(n)) = \{ f(n) : 모든 \ n\ge n_0에 \ 대해 \ 0\le f(n) \le cg(n)인 \ 양의 \ 상수 \ c, \ n_0이 \ 존재한다.\} $$
$O(g(n))$ 을 살펴보면, $f(n)$을 중괄호로 감싸고 있다. 이는 집합을 나타내는 기호이다.
즉, $O(g(n))$은 특정 조건을 만족하는 $ f( n)$의 집합이라고 볼 수 있기 때문에 $f(n)\in O(g(n))$ 이며, $f(n) = O(g(n))$ 라고 표현할 수 있다. 이는 다른 notation에도 동일하게 적용된다.
그렇다면 O-notation의 특정 조건은 무엇일까?
간단히 말하면, 충분히 큰 양의 상수 $n$ 과 양의 상수 $c$ 에 대한 $0\le f(n) \le cg(n)$ 이다.
이를 만족하는 경우, $g(n)$ 은 $f(n)$ 에 대하여 **점근적 상한(asymptotic upper bound)**이다.
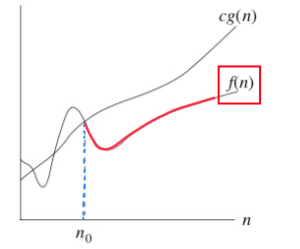
예시로, 아래의 그래프를 통해 $c = 1, \ n_0 = 2$ 라는 조건 하에 $2n^2 = O(n^3)$ 이라는 결과를 도출할 수 있다.

그 외에 자주 사용되는 시간에 따른 그래프 비교는 아래와 같다.

[$\mathsf{\Omega}$-notation]
$$ \mathsf{\Omega}(g(n)) = \{ f(n) : 모든 \ n\ge n_0에 \ 대해 \ 0\le cg(n) \le f(n) \ 양의 \ 상수 \ c, \ n_0이 \ 존재한다.\} $$
$\mathsf{\Omega}$-notation의 특정 조건은 무엇일까?
충분히 큰 양의 상수 $n$ 과 양의 상수 $c$ 에 대한 $0\le cg(n) \le f(n)$ 이다.
이를 만족하는 경우, $g(n)$ 은 $f(n)$ 에 대하여 **점근적 하한(asymptotic lower bound)**이다.

예시로, 아래의 그래프를 통해 $c = 1, \ n_0 = 16$ 이라는 조건 하에$\sqrt n = \mathsf{\Omega}(lg \ n)$ 이라는 결과를 도출할 수 있다.

[$\mathsf{\Theta}$-notation]
$$ \mathsf{\Theta}(g(n)) = \{ f(n) : 모든 \ n\ge n_0에 \ 대해 \ 0 \le c_1g(n) \le f(n) \le c_2g(n)인 \ 양의 \ 상수 \ c_1, \ c_2, \ n_0이 \ 존재한다.\} $$
$\mathsf{\Theta}$-notation의 특정 조건은 무엇일까?
충분히 큰 양의 상수 $n$ 과 양의 상수 $c_1$, $c_2$에 대한 $0 \le c_1g(n) \le f(n) \le c_2g(n)$ 이다.
이를 만족하는 경우, $g(n)$ 은 $f(n)$ 에 대하여 **점근적으로 엄밀한 한계(asymptotic tight bound)**이다.
즉, 상한과 하한 사이에 낀 구조이기 때문에 아래와 같이 표현하는 것도 가능하다.
$$ f(n) = \mathsf{\Theta}(g(n)) \iff f = O(g(n)) \ and \ f = \mathsf{\Omega}(g(n)) $$
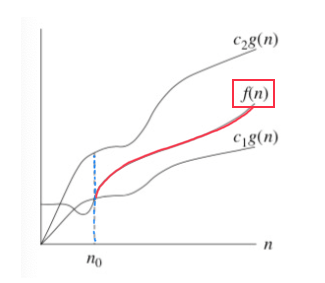
예시로, 아래의 그래프를 통해 $c_1 = {1 \over 4}, \ c_2 = {1 \over 2}, \ n_0 = 8$ 이라는 조건 하에 ${n^2 \over 2} - 2n = \mathsf{\Theta(n^2)}$ 이라는 결과를 도출할 수 있다.

다음은 little notation에 대해 알아볼 것이다.
[o-notation]
앞선 Big-oh notation에서 $2n^2 = O(n^2)$는 점근적으로 정확하지만, $2n = O(n^2)$ 는 그렇지 않다.
그래서 o-notation은 점근적으로 여유있는 상한을 나타내기 위해 사용된다.
$$ o(g(n)) = \{ f(n) : 임의의 \ 양의 \ 상수 \ c>0에 \ 대해, \ 그리고 \ 모든 \ n \ge n_0에 \ 대해 \ 0\le f(n) < cg(n)인 \ 양의 \ 상수 \ n_0이 \ 존재한다.\} $$
예를 들어, $2n^2 \ne O(n^2)$ 이지만, $2n = O(n^2)$이다.
혹은 이렇게 표현하는 것도 가능하다.
$$ \lim_{n \to \infty} {f(n)\over g(n)} = 0 $$
이에 해당하는 예시는 아래이다.
$n^{1.9999} = o(n^2)$
${n^2 \over lg n} = o(n^2)$
${n2 \over 1000} \ne o(n^2)$
[$\mathsf{\omega}$-notation]
$\mathsf{\omega}$-notation은 점근적으로 여유있는 하한을 나타내기 위해 사용된다.
$$ \mathsf{\omega}(g(n)) = \{ f(n) : 임의의 \ 양의 \ 상수 \ c>0에 \ 대해, \\ 그리고 \ 모든 \ n \ge n_0에 \ 대해 \ 0\le cg(n) < f(n)인 \ 양의 \ 상수 \ n_0이 \ 존재한다.\} $$
이에 해당하는 예시는 아래이다.
$n^{2.0001} = \mathsf{\omega}(n^2)$
$n^2 \ lg\ n = \mathsf{\omega}(n^2)$
$n^2 \ne \mathsf{\omega}(n^2)$
이렇게 점근적 표기법을 알아보았다.
그러나 나와 같은 평범한 사람들에게는 조금 난해하게 느껴질 수도 있다.
사실 조금 더 쉽게, 다음과 같이 정리할 수 있다.
$$ f(n) = O(g(n)) \qquad is \ \ like \qquad a \le b, \\ f(n) = \mathsf{\Omega}(g(n)) \qquad is \ \ like \qquad a \ge b, \\ f(n) = \mathsf{\Theta}(g(n)) \qquad is \ \ like \qquad a = b, \\ f(n) = o(g(n)) \qquad is \ \ like \qquad a < b, \\ f(n) = \mathsf{\omega}(g(n)) \qquad is \ \ like \qquad a > b. \\ $$
( * 숫자들과 다르게 모든 함수들이 점근적으로 비교 가능한 것은 아니다.)
'CS > 알고리즘' 카테고리의 다른 글
| [Introduction to Algorithms] 4. 분할정복 (0) | 2022.02.14 |
|---|---|
| [Introduction to Algorithms] 2. 시작하기 (0) | 2022.02.02 |
| [Introduction to Algorithms] 1. 알고리즘의 역할 (0) | 2022.02.02 |
| 유클리드 알고리즘 (Euclid’s algorithm) (0) | 2021.11.03 |



